动态规划(DP:Dynamic Programming)

是运筹学的一个分支，是求解决策过程(decision process)最优化的数学方法。在面试笔试中动态规划也是经常作为考题出现，其中较为简单的DP题目我们应该有百分之百的把握顺利解决才可以。

动态规划的定义

动态规划实际上是一类题目的总称，并不是指某个固定的算法。动态规划的意义就是通过采用递推（或者分治）的策略，通过解决大问题的子问题从而解决整体的做法。动态规划的核心思想是巧妙的将问题拆分成多个子问题，通过计算子问题而得到整体问题的解。而子问题又可以拆分成更多的子问题，从而用类似递推迭代的方法解决要求的问题。

无后效性

无后效性是指如果在某个阶段上过程的状态已知，则从此阶段以后过程的发展变化仅与此阶段的状态有关，而与过程在此阶段以前的阶段所经历过的状态无关。利用动态规划方法求解多阶段决策过程问题，过程的状态必须具备无后效性。

最优子结构

一个最优化策略具有这样的性质，不论过去状态和决策如何，对前面的决策所形成的状态而言，余下的诸决策必须构成最优策略。简而言之，一个最优化策略的子策略总是最优的。一个问题满足最优化原理又称其具有最优子结构性质。

动态规划解题步骤

1. 状态的定义
2. 状态转移方程的定义

状态的定义

有的问题过于的抽象,或者一大堆文字,这严重的干扰了我们的阶梯思路,所以我们就将这一段话进行一下数学抽象转化成一个数学问题

比如:

题目:求一个数列中最大连续子序列的和

所以我们可以将这个问题转化成

状态定义:F(k)是第k项钱的最大序列和,求F(1)到F(n)中的最大值

我们这一转换就将一个相对模糊的问题转换成了一个相对清晰的数学问题,我们就将这一过程叫做状态定义,这样的状态定义给出了一种类似通解的思路,把一个毫无头绪的问题转换成了一个可以求解的问题

状态方程的定义

我们进行了状态定义之后,就会去想到求解F(1)到F(n)中的最大值,而状态转移方程的定义则是告诉我们该如何去解决这一个转换后的数学问题

对于上述我们已经转换成一个数学问题,我们需要关注的点就在于,如何能够用前一项或者前几项的信息得到下一项,这种从最优子状态转换成下一个最优状态的思路就是动态规划的核心

F(k) = max {F(k-1)+A(k),A(k)}
F(k)是前K项的和,A(k)是第K项的值

动态规划应用的场景

对于一个可以拆分的问题中存在可以由前若干项计算当前项的问题可以由动态规划进行计算

数塔取数问题

一个高度为N的由正整数组成的三角形，从上走到下，求经过的数字和的最大值。
每次只能走到下一层相邻的数上，例如从第3层的6向下走，只能走到第4层的2或9上。
该三角形第n层有n个数字，例如：
第 一 层 有一个数字： 5
第 二 层有两个数字： 8 4
第 三层有三个数字： 3 6 9
第四层有四个数字：7 2 9 5
最优方案是：5 + 8 + 6 + 9 = 28
注意:上面应该是排列成一个三角形的样子不是竖向对应的，排版问题没有显示成三角形。

状态定义: Fi，j是第i行j列项最大取数和，求第n行Fn，m（0 < m < n）中最大值。

状态转移方程：

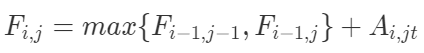
PS:MD解析有点问题,始终解析不出来这个公式

package dp;

import java.util.Scanner;

/**
 * >一个高度为N的由正整数组成的三角形，从上走到下，求经过的数字和的最大值。
 * >每次只能走到下一层相邻的数上，例如从第3层的6向下走，只能走到第4层的2或9上。
 * >该三角形第n层有n个数字，例如：
 * >第一层有一个数字：   5
 * >第二层有两个数字：  8 4
 * >第三层有三个数字： 3 6 9
 * >第四层有四个数字：7 2 9 5
 * >最优方案是：5 + 8 + 6 + 9 = 28
 * >注意:上面应该是排列成一个三角形的样子不是竖向对应的，排版问题没有显示成三角形。
 */

public class Main {
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        int n = scan.nextInt();
        long max = 0;
        int[][] dp = new int[n][n];
        dp[0][0] = scan.nextInt();

        for (int i = 1; i < n; i++) {
            for (int j = 0; j <= i; j++) {
                int num = scan.nextInt();
                if (j == 0) {
                    //根据状态方程这是最左边的,就只有一种情况
                    dp[i][j] = dp[i - 1][j] + num;
                } else {
                    dp[i][j] = Math.max(dp[i - 1][j - 1], dp[i - 1][j]) + num;
                }
                max = Math.max(dp[i][j], max);
            }
        }
        System.out.println(max);
    }
}

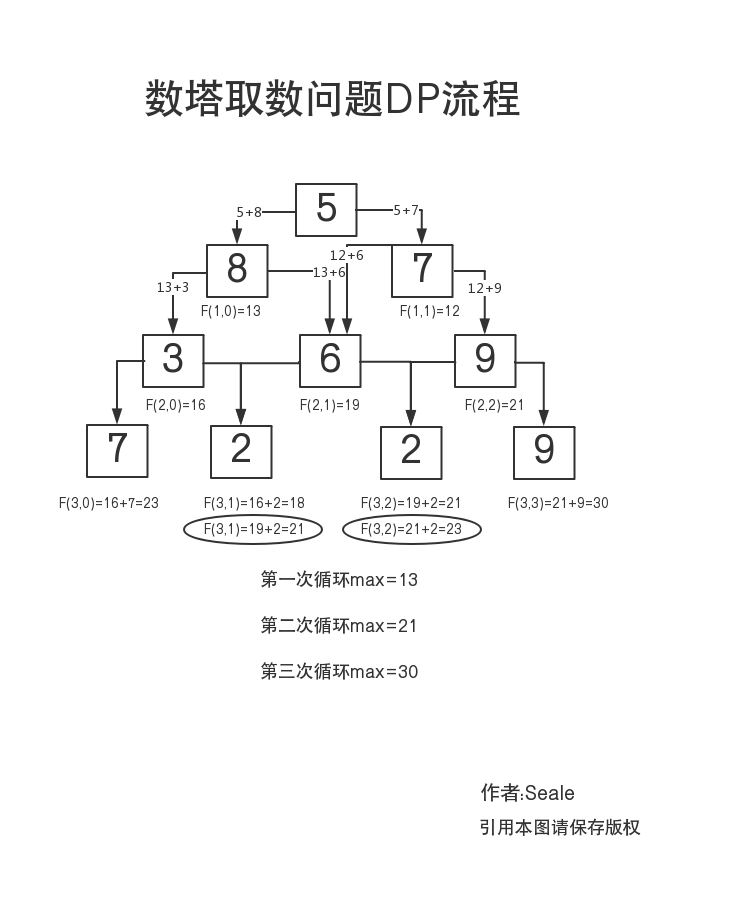
我做了一个流程图以方便理解,数值我更改了一下为

        5
      8   7
    3   6   9
  7   2   2   9

显而易见,最优路径为5+7+9+9=30